
Andymath.com features free videos, notes, and practice problems with answers! Printable pages make math easy. Are you ready to be a mathmagician?


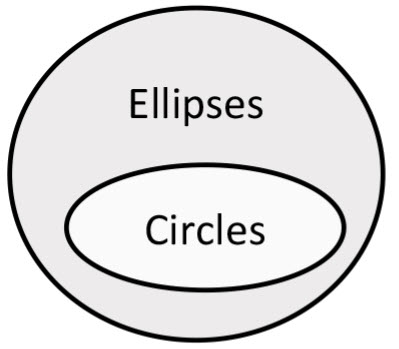 Venn Diagram Solution to Question Number 7" width="200" height="175" />
Venn Diagram Solution to Question Number 7" width="200" height="175" />
One example below
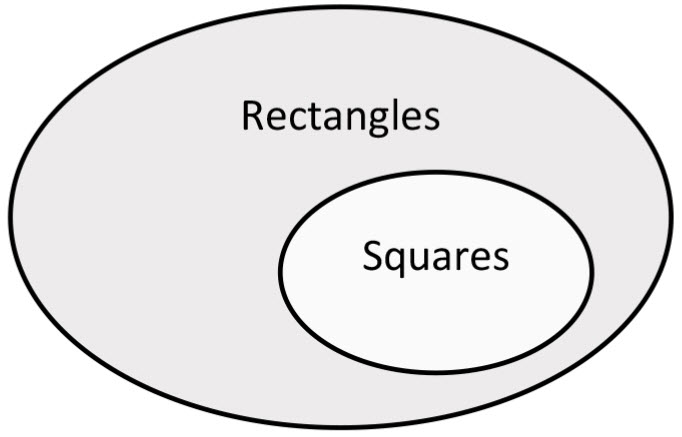
 Venn Diagram Solution to Question Number 8" width="200" height="175" />
Venn Diagram Solution to Question Number 8" width="200" height="175" />
Note it is the same answer as number 7. They are equivalent statements.
“If a square, then a rectangle.” or “All squares are rectangles”
and
“If not a rectangle, not a square.” or “All non-rectangles are non-squares”
 Venn Diagram Solution to Question Number 9" width="341" height="219" />
Venn Diagram Solution to Question Number 9" width="341" height="219" />
The converse of a conditional statement is formed by flipping the order in which the hypothesis and conclusion appear. For example, the converse of the statement “If it is raining, then the ground is wet” is “If the ground is wet, then it is raining.”
The inverse of a conditional statement is formed by negating both the hypothesis and conclusion. For example, the inverse of the statement “If it is raining, then the ground is wet” is “If it is not raining, then the ground is not wet”
The contrapositive of a conditional statement is formed by negating both the hypothesis and conclusion and flipping the order in which they appear. For example, the contrapositive of the statement “If it is raining, then the ground is wet” is “If the ground is not wet, then it is not raining.”
A biconditional statement is a statement in the form “If and only if P, then Q,” which is equivalent to the statement “P if and only if Q.” This means that P and Q are either both true or both false. For example, the statement “If and only if it is raining, the ground is wet” is a biconditional statement.
In geometry class, students learn about conditional statements and their related concepts (inverse, converse, contrapositive, and biconditional) in order to make logical deductions about geometric figures and their properties. These concepts are often used to prove theorems and solve problems.
Andymath.com is a free math website with the mission of helping students, teachers and tutors find helpful notes, useful sample problems with answers including step by step solutions, and other related materials to supplement classroom learning. If you have any requests for additional content, please contact Andy at tutoring@andymath.com. He will promptly add the content.
Visit me on Youtube, Tiktok, Instagram and Facebook. Andymath content has a unique approach to presenting mathematics. The clear explanations, strong visuals mixed with dry humor regularly get millions of views. We are open to collaborations of all types, please contact Andy at tutoring@andymath.com for all enquiries. To offer financial support, visit my Patreon page. Let’s help students understand the math way of thinking!
Thank you for visiting. How exciting!